online

gaaanz unten

H 57 a

divergenz für alpha < 11/3

›keine ahnung‹ für alpha = 11/3 

konvergenz für 11/3 < alpha < 13/3

›keine ahnung‹ für alpha = 13/3

divergenz für alpha > 13/3

H 57 b

konvergenz für alpha = 11/3 ... siehe leibniz-kriterium

divergenz für alpha = 13/3 ... siehe harmonische reihe

H 58 a

als ›konvergente majorante‹ kann ... 

summe [ n gleich null bis unendlich ] 1/2 hoch n

... benutzt werden

H 58 b und c

H 59 a

summe [ n gleich null bis unendlich ] 1/16 hoch n

+

1/2 mal summe [ n gleich null bis unendlich ] 1/4 hoch n

= 16/15 + 1/2 · 4/3 = 26/15

H 59 b

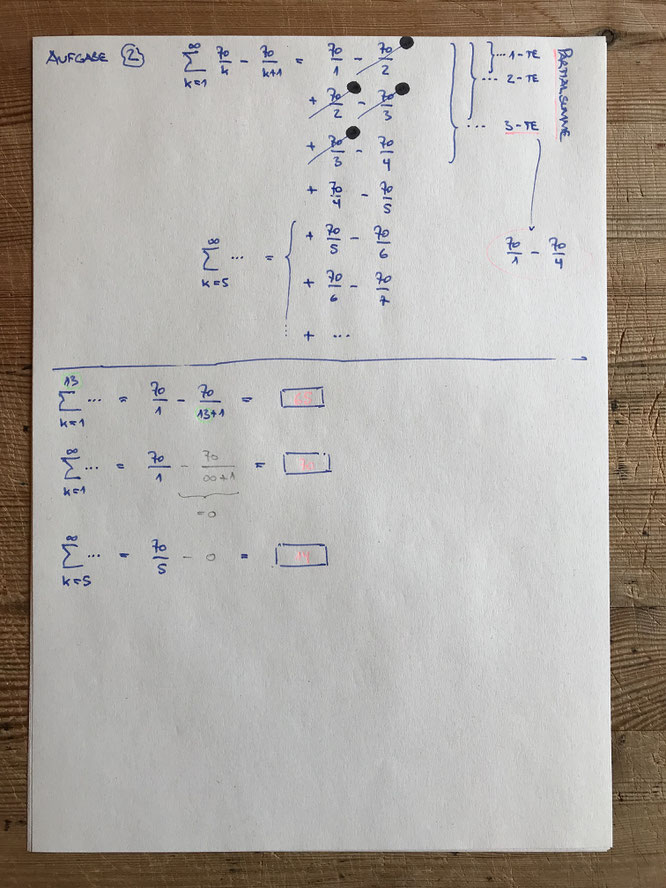
es handelt sich um eine ›teleskopsumme‹

– 1/2 – 2/3 + 1 + 1 = 5/6

H 60 a

konvergent ... mit quotienten-kriterium

H 60 b

divergent ... nach partialsummenbetrachtung

H 60 c

divergent ... mit wurzel-kriterium (vgl. auch H 55c)

außerdem bilden die summanden a_n keine nullfolge

oberer teil des fotos

H 60 d

konvergent ... mit wurzel-kriterium

unterer teil des fotos

online

ich löse die folgenden beispielaufgaben

die angegebene anleitung sollte sich mühelos auf ›andere zahlenwerte‹ anwenden lassen